La funzione TENDENZA di Excel a supporto delle decisioni aziendali

In questa saggio analizziamo, dopo una breve esposizione di semplici concetti matematici, la struttura e le potenzialità in termini di calcolo della funzione statistica TENDENZA di Excel e le possibilità di un suo proficuo utilizzo in ambito aziendalistico.

Supponiamo di avere dei punti sugli assi cartesiani come raffigurato nell’immagine sottostante.

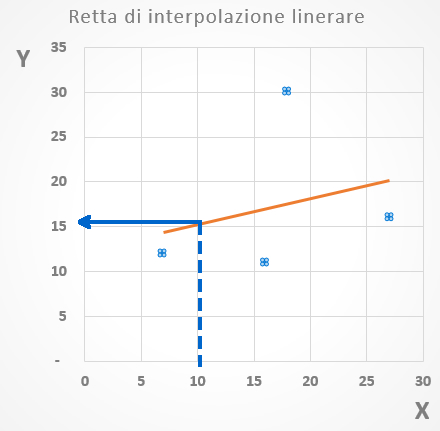
La funzione TENDENZA calcola automaticamente l’equazione della retta di interpolazione lineare utilizzando il “metodo dei minimi quadrati” (la retta disegnata nel grafico) e restituisce il valore Y di questa retta corrispondente ad un valore X indicato dall’operatore.

Nell’esempio riportato, se intendiamo conoscere il valore Y corrispondente ad X=10, la funzione TENDENZA restituirà un valore pari a 15; diversamente, se intendiamo conoscere il valore Y corrispondente ad X=25, sarà restituito un valore di poco inferiore a 20.

La funzione, che appartiene alla categoria Statistiche, ha la seguente sintassi:

=TENDENZA(y_nota;x_nota;nuova_x;cost)

Il primo argomento (y_nota) indica l’insieme dei valori Y noti, mentre il secondo (x_nota) l’insieme dei valori X noti (questi valori serviranno ad Excel per calcolare la funzione della retta di interpolazione); il terzo argomento (nuova_x) indica il valore X del quale si intende conoscere il corrispondente valore di Y (l’applicazione andrà a sostituire alla retta di interpolazione creata Y=mx+q, il valore X per determinare il valore Y); l’ultimo argomento (cost) è un valore logico: se corrisponde a Falso, la retta di interpolazione viene fatta passare per l’origine ovvero viene calcolata secondo la formula Y=mx, mentre se corrisponde a VERO oppure è omesso (nella maggior parte dei casi), la funzione della retta di interpolazione viene calcolata normalmente secondo la formula Y=mx+q.

Esempi di applicazione della funzione TENDENZA in ambito aziendalistico

Ma vediamo ora come questa funzione, che sembrerebbe studiata apposta per i “matematici”, può essere facilmente utilizzata anche in ambito aziendalistico.

Esempio 1

Supponiamo di avere a disposizione nelle celle A2:A6 le quantità prodotte nel reparto A di un’impresa degli ultimi cinque anni e nelle celle B2:B6 la spesa per i “corsi di addestramento del personale” sostenuti negli stessi esercizi; supponiamo inoltre che sussista una certa relazione tra le quantità prodotte e i corsi frequentati dai dipendenti e di voler conoscere quanti prodotti verranno realizzati nel prossimo anno (variabile dipendente Y) a fronte di una spesa di 10.000,00 EUR in “corsi di addestramento” (variabile indipendente X).

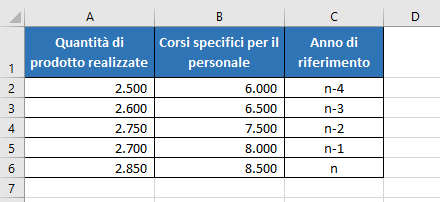
Matematicamente dovremmo costruire un grafico assegnando all’asse Y le quantità prodotte dal reparto A e all’asse X la spesa per i corsi di addestramento e, dopo aver determinato l’equazione della retta di interpolazione (attraverso “il metodo dei minimi quadrati”) dovremmo calcolare il corrispondente valore Y (la previsione delle quantità prodotte nell’esercizio n+1) sostituendo nell’equazione della retta il valore X con 10.000. Tutto questo può essere fatto con la funzione TENDENZA utilizzando la seguente sintassi:

=TENDENZA(A2:A6;B2:B6;10000)

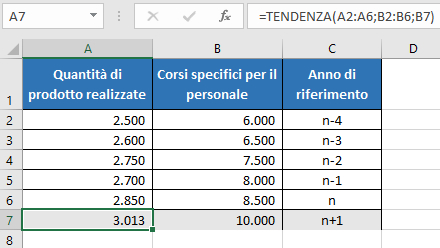
Se la previsione di spesa per i corsi la inseriamo nella cella B7 della tabella, nella cella A7 la funzione TENDENZA farà riferimento a tale cella, anziché al valore numerico 10.000

=TENDENZA(A2:A6;B2:B6;B7)

Esempio 2

Supponiamo invece, sempre facendo riferimento ai dati dell’esempio precedente, di voler conoscere a quanto dovrà ammontare la spesa in corsi di addestramento per ottenere una produzione complessiva di 4.000 pezzi.

In questo caso, la variabile indipendente (variabile X) è data dalle quantità prodotte, mentre la variabile dipendente (variabile Y) è data dalla spesa in corsi di addestramento: il grafico, pertanto, dovrebbe essere costruito invertendo le coordinate. Di conseguenza, la sintassi della funzione dovrà essere la seguente:

=TENDENZA(B2:B6;A2:A6;4000)